Survival Analysis: Censoring of Data

Imagine yourself to be a Data Analyst in a travel agency.

Your task is, in a given duration of time T, you need to gather customers data, make an analysis and come up with a business plan which has a target of “persuading customers for at least one travel plan with your company”. Your target is fulfilled only when the customer plans for one travel destination in association with the travel agency. You need to get the time duration from the start after which the customer books a travel plan (Known as Survival Time, discussed later in the post).

So let's consider that one of the following three events has occurred in that time duration,

1. The time duration T ends and the particular customer did not plan one travel.
2. The customer is lost to follow up in the time duration T.
3. The customer withdraws from the study (due to some reasons).

For the first case, the study ends and the customer has no travel plan. This data speaks very less about the customer’s plan and doesn’t confirm if a travel plan was booked. For example, the study is being conducted for four months(June-Sept.) and the customer did not book a plan during those four months. After two months (Dec.) there comes one planning from the customer side with the travel agency. In this case, the target of at least one travel plan is fulfilled but not within the time limit.

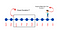
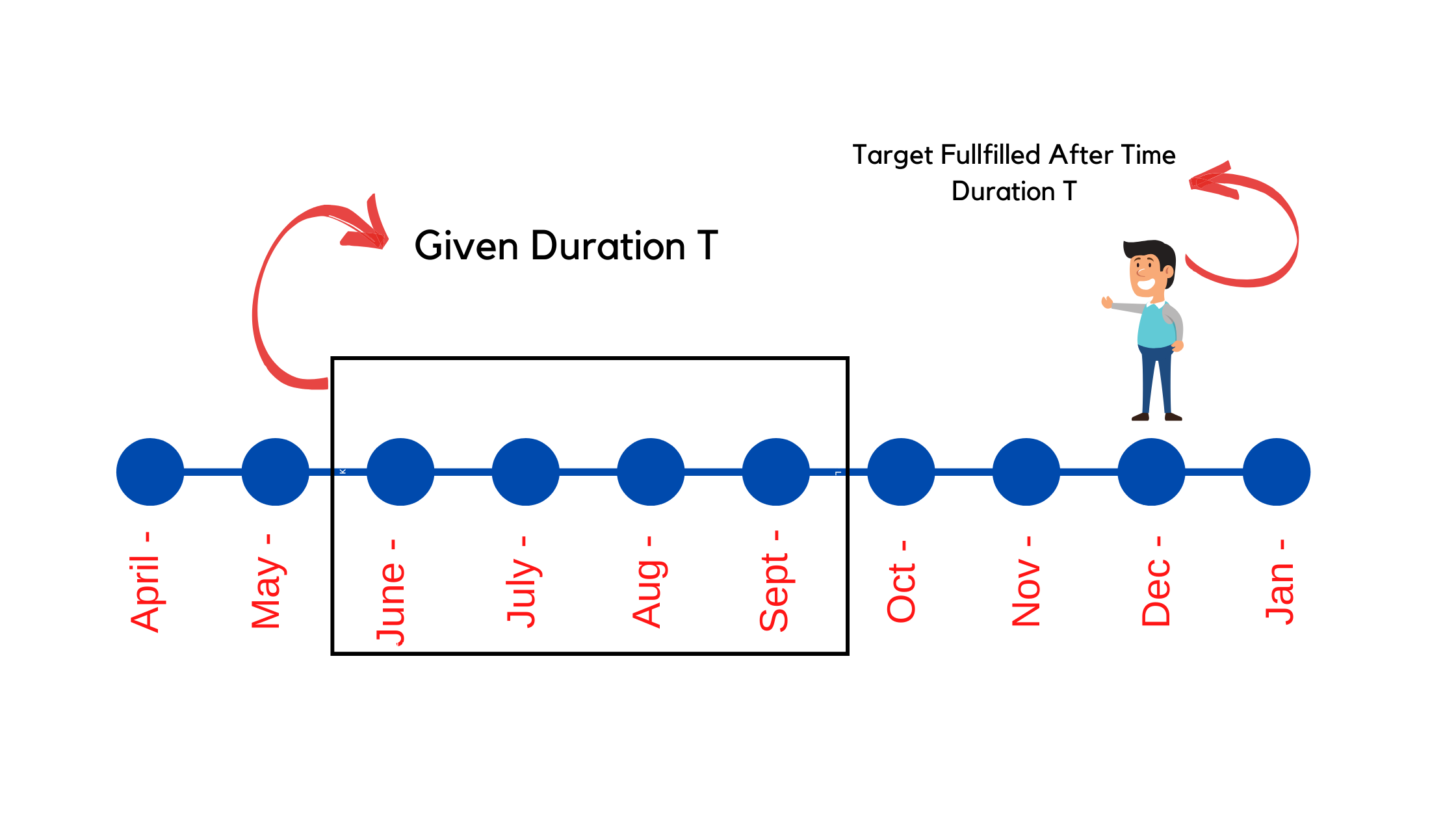
Time Duration T ends and The Target is fulfilled after time T

For the second case, in the given time duration T, the customer data may be lost to follow up due to some reasons. In general, companies provide surveys, feedbacks and other forms to get the required data from the customer but if anyhow it fails (like the customer doesn’t fill the form or the form wasn’t delivered), then there is a follow-up failure and the customer is lost during that period. Again this doesn’t confirm exactly if the target is going to be fulfilled later. Suppose the customer books a travel plan in November, but that can’t be confirmed from the data available during the duration T.

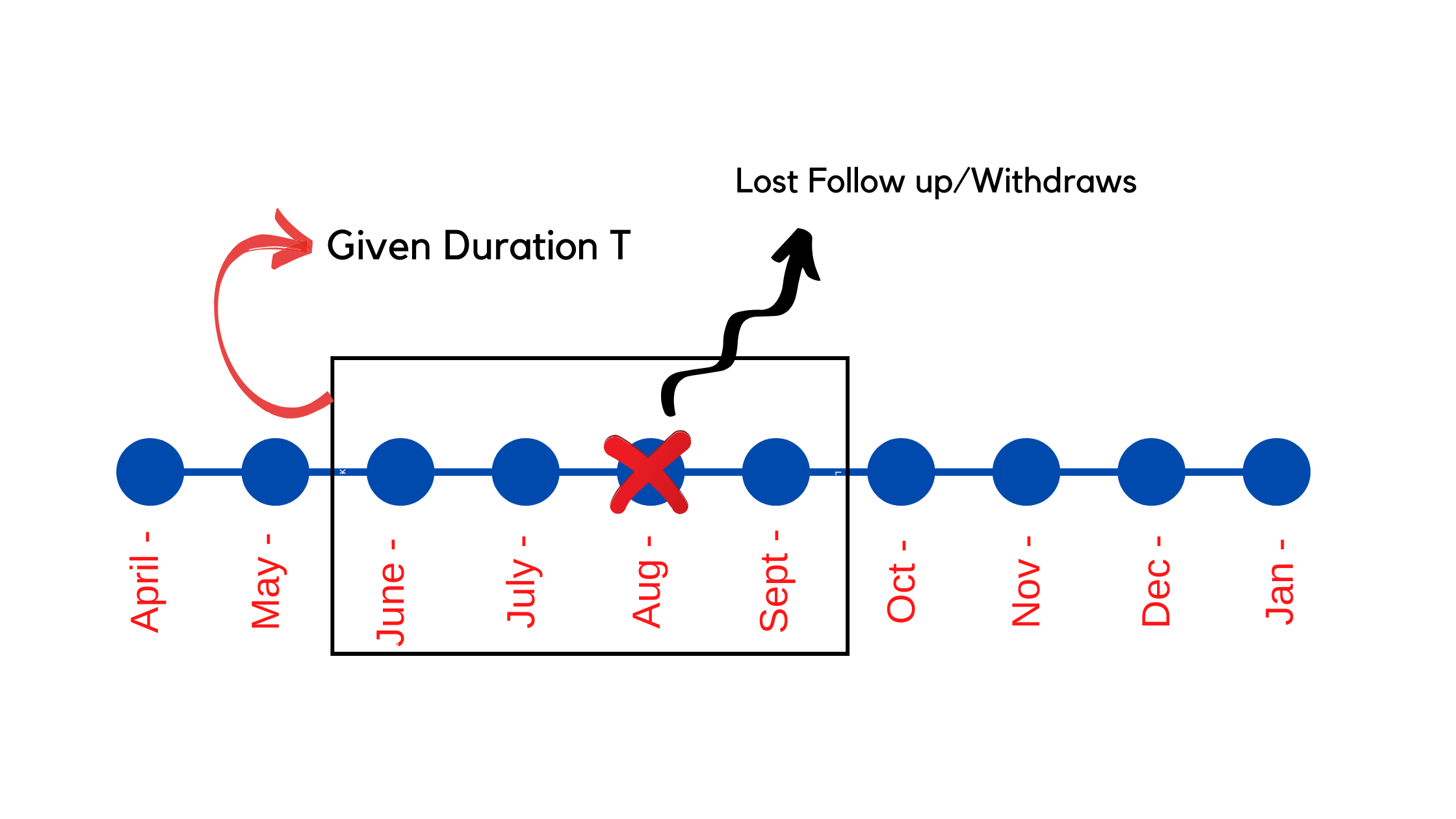
Lost Follow up / Withdraw before the duration T

The third case is a very common one, there are several reasons that directly and indirectly enforce the customer to withdraw. The reasons include getting some better plans from other travel companies or the customer starts facing some economical issues etc. But these reasons are temporary. The customer withdraws during the duration T but may return back after some time to make a travel plan.

So the three cases above don't exactly speak about the Survival Time, i.e. time taken to fulfil the target after being started.

What is Survival Time and Censored Data?

For any data set, when our focus becomes the “time until an event occurs”, we call that time as the Survival Time for that particular data point.

The event can be anything ranging from death, getting cured of a disease, staying with a business or time taken to pass an exam etc.

By the time, we mean years, months, weeks, or days from the beginning of follow-up of an individual until an event occurs.

Censoring is a key phenomenon of Survival Analysis in Data Science and it occurs when we have some information about individual survival time, but we don’t know the survival time exactly.

For example, in the above illustration of travel agency, for the three cases described, we have some data about a particular customer but that was not enough to determine the time taken by that customer to fulfil the target or give back a failure (doesn’t even fulfil the target at all). We call this phenomenon as Censoring of Data and this type of data is known as Censored Data.

Types of Censored Data:

Well, basically there are two types of Censored Data, one is “Right Censored” and the other one is “Left Censored”. Both of these can be explained using a basic model of interval-censored data.

Suppose we have a time duration from t1 to t2, where t1 is the starting time and t2 is the target achieved time. In some cases, the event occurs in between t1 and t2 and it’s not possible to determine exactly when the event has occurred. For example, there is a man who came to the hospital to check if he is attacked by COVID-19. He tests negative. But as the incubation period of the Coronavirus is about 15 days, he comes again after 15 days to test and this time it’s positive.

Although the target is achieved, still the exact timing is unknown, he might be got affected any day in between those 15 days. Hence survival time can not be determined exactly. This type of data is known to be interval-censored.

So we can define Survival analysis data is known to be interval-censored, which can occur if a subject’s true (but unobserved) survival time is within a certain known specified time interval.

Now suppose t1 is zero, For example, suppose the person tries COVID test during the initial stage of the spread of this pandemic (mapping the time to zero) and tests negative. After around three months he returns to test again and this time tests positive. The target event was to test COVID positive. Although that has occurred at a time t2 (after three months), but still the exact time of getting affected by the virus is unknown. It can be any time between 0 and t2. This type of data is known as left-censored.

So we can define left-censored data can occur when a person’s true survival time is less than or equal to that person’s observed survival time.

Again considering the same case, let t1 be the first time when the person tests negative and t2 be upper bound of the time duration given to us. Suppose the person did not test positive during t1 and t2. This doesn’t fulfil the target between the given time duration but there may be a situation after some days (after t2), that the person tests positive. Simply speaking, the target is achieved but after the time duration given for the model. This type of data is known as right-censored. Most of the survival analysis datasets are right-censored due to the three major reasons given above in the travel agency example.

If the person’s true survival time becomes incomplete at the right side of the follow-up period, occurring when the study ends or when the person is lost to follow-up or is withdrawn, we call it as right-censored data.

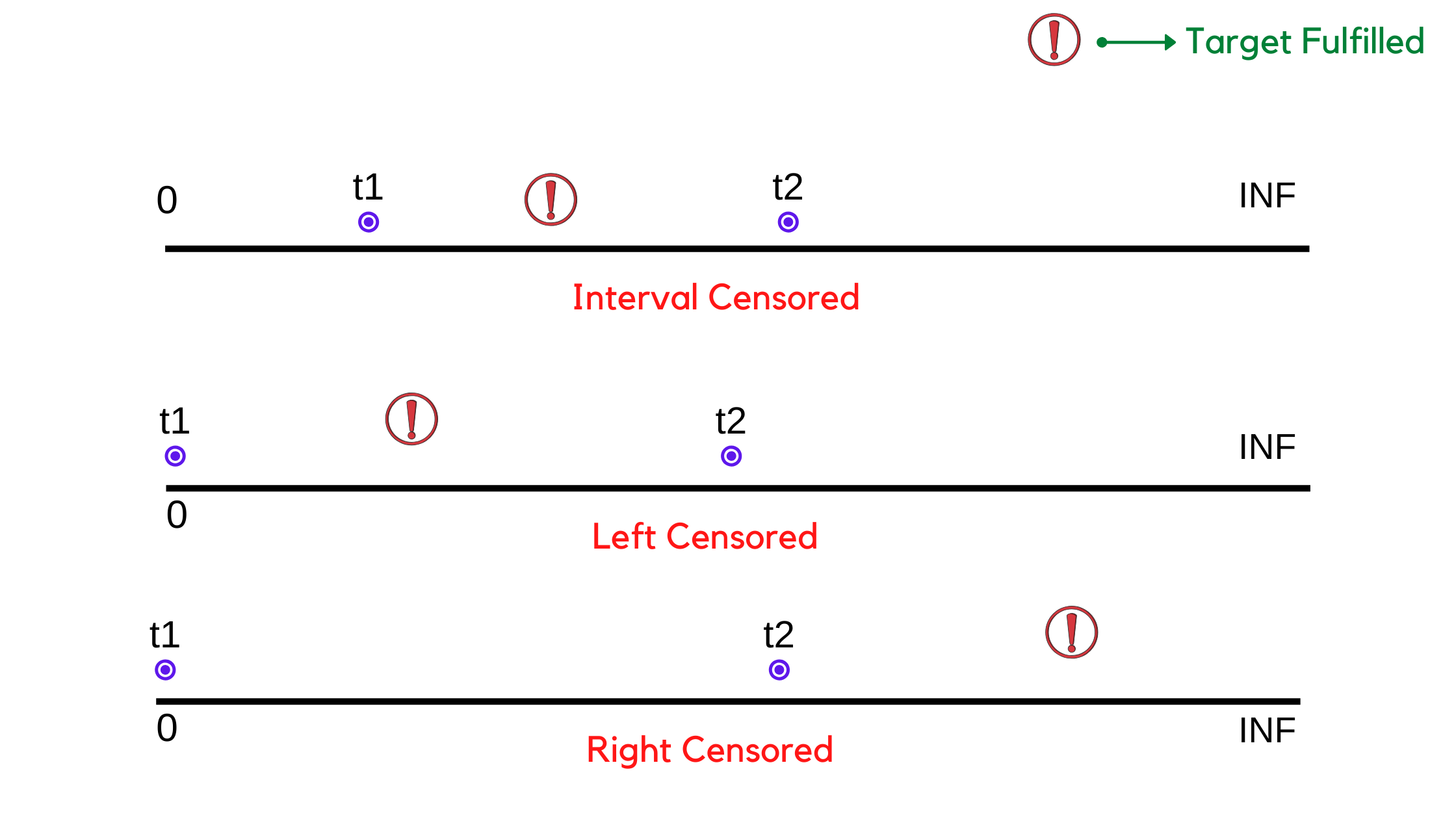
Pictorial Intuition of Censored Data

[PS- This article is written as a part of SCI-2020 program by scodein.tech, for the open-sourced project named — “Survival Analysis”]